job-recommender
Recommend jobs using collaborative filtering and ALS.
job-recommender
A Job Recommendation Engine with Implicit Feedback. Two models are developed. The first used content-based filtering; the second implemented Collaborative Filtering for Implicit Feedback. Collaborative Filtering algorithms tries to capture the commonality between users.
Project Intro
Develop a model to recommended jobs to users on a job portal. The dataset contains only implicit feedback thus algorithm that requires explicit feedback such as rating and user reviews are not applicable.
Methods Used
- Natural Language Processing
Technologies
- Python
- Python pandas, seaborn, regex
- Python scikit-learn
Project Description
job_recommender.ipynb- TfidfVectorizer transforms text to feature vectors that can be used as input to estimator. Content-based filtering - job description based recommender (recommend jobs based on highest cosine similarity), similar user based recommender (recommend jobs of similar users).job_als.ipynb- Alternating Least Square (ALS) algorithm is chosen since the dataset only contains implicit feedback. Python Implicit library made implementing the complex algorithm simpler and faster. ALS measures the confidence whether a user will apply for a job based on a constructed Matrix. The Matric factorises jobs and users into features. ALS algorithm keeps on refining the values based on training set.
Implicit vs explicit data
Explicit data for example like, ratings.
Implicit data (data what we have) is data gathered from user behaviour, e.g. click history, number of views, time spent. We have more of this data but it is not always clear what it means.
Use SVD for predicting explicit data. Use ALS for predicting implicit data.
Alternating Least Squares (ALS)
We’ll fit our data to ALS and find similarities. The idea is to take a large matrix and factor it into a smaller representation (lower dimensional matrices). These dimensions are called latent or hidden features that are learned from data.
The difference with explicit data lies in how we deal with missing data in the sparse matrix. For explicit data we can treat them as unknown fields that we are predicting. But for implicit data we cannot know whether a user liked or disliked the missing value.
Computing U and P through ALS
The goal of ALS is to find two matrices U and P, such that their product is approximately the original matrix of users and products.
Alternate:
- fix matrix U and find the optimal matrix P
- fix matrix P and find the optimal matrix U
Similar items
Similarity between items can be computed by the dot-product between P vectors and it’s transpose.
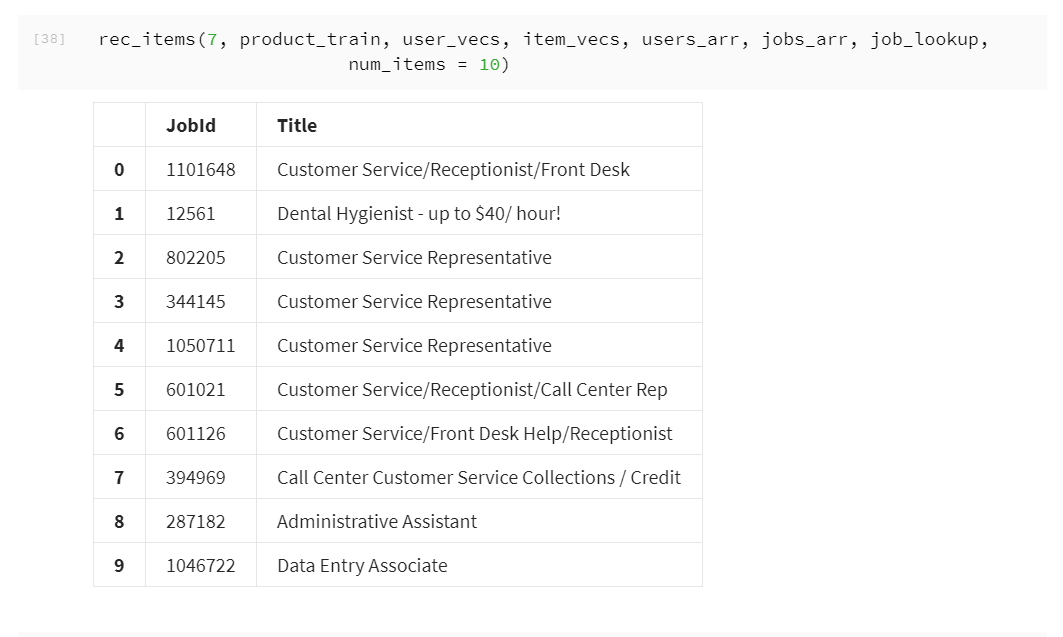
Making recommendations
Dot product between user vector and the transpose of product vector.
Data source from Kaggle CareerBuilder.
Process Flow
- data processing/cleaning
- text processing
- words tokenizing
- model training
Reference
ALS Implicit Collaborative Filtering
A Gentle Introduction to Recommender Systems with Implicit Feedback
Finding Similar Music using Matrix Factorization
Future Improvement
Inlcude evaluation.